Hello, non-coder person! If you are not a developer and clicked on this article anyway, thank you! This article is definitely aimed at you. I’m a firm believer in cross-pollination and synergy among different disciplines and to that end, I have written this article to provide a bit of insight into the world of logic as developers see it on a daily basis.
My hope is to illustrate a fundamental concept in development that is important to all of us who rely on our work being correct, timely and self-evaluating. It is my intention to explain something in pseudo-coding terms that provides immediate value to all Agile teams. Understanding the nuances of logical decision trees like those developers create can help improve the way we organize our projects, communicate our needs and execute our tasks on a daily basis. Follow along, won’t you??
And if you like this article, please have a look at my developing Agile article series, Continuous Learning Curve!
Wanted: True or False
The most basic concept in the world of coding is logic, and logic is binary. Statements can either be evaluated as true, or as false. There are no “maybe’s” in logic. It is a world of seeming perfect bifurcation: true and false, one and zero, on and off.
One might think that a binary system’s best expression would be a perfectly-bisected world: a world in which concepts evaluate as true as often as they do false. One would expect code created in this world would work as effectively on both sides of the boolean divide.
But that seeming clarity hides a world of complexity, as new developers quickly discover. Nothing about the duality of logic creates a truly binary system, because the concept of false encompasses a world of bad options much larger than that of true: anything in the world other than true is false.
Should I Stay or Should I Go (a boolean example)?
Consider a simple mathematical equation: 2 + 2 = x. If I were to tell you that x was 4, that would be true. But every other number you can think of is false. So to would be every alphanumeric character, punctuation mark and combination of characters. The number of true statements (1) is vastly outweighed by incorrect statements (∞-1).
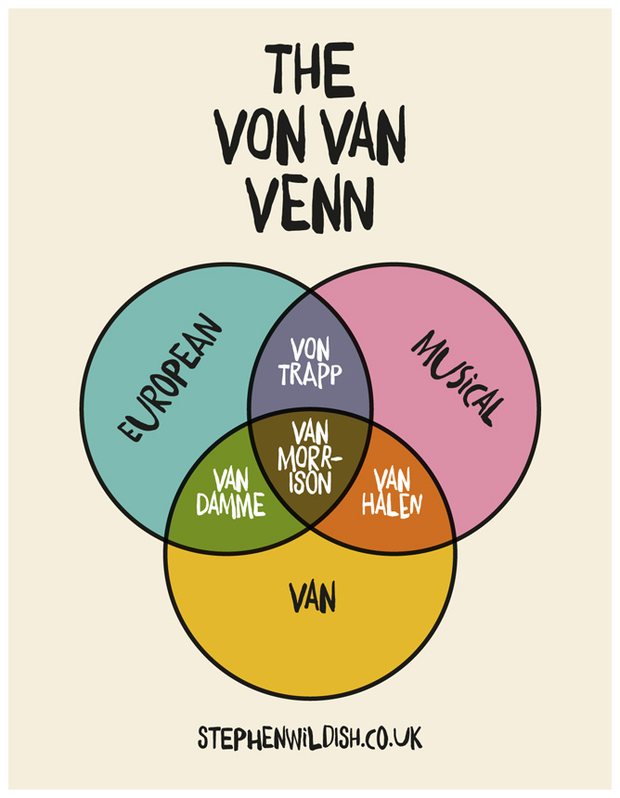
Fig. 1 – Save this image and take notes. This is important.
source:imgur.com
Of course, that is a simple example. As a slightly more complex example, consider the Venn diagram to the left.
How would we construct a logical statement from this diagram that could evaluate to true or false? Well, what if we were to ask “Is a Van musical?” The human answer is “maybe.” And the answer is a maybe, based on other data: is the Van in question a Van Halen, or some other type of Van? Because if it’s a Van Damme, well, that’s not musical at all, according to the chart. A computer will therefore evaluate the answer as “false,” because simply being a Van is not enough to be musical.
Yet in this more complex example, the ranges of potentially true and false statements are much narrower and much closer to equal than in the simple algebraic one. We do not have a single right answer and because we are bound by three domains (European, Musical and Van) we do not have an infinite number of answers, either. We do have answers that are partially correct, and evaluating the veracity of any statement based on this example gets trickier.
Most Musical people and European people are not Vans, but even most Vans are not Musical. Meanwhile all intersections between the Musical and the Van circles – including that section where all three circles intersect – evaluate as true. We’ll call that center bit the “Van Morrison Zone.”
Decisions in the Boolean World
Decision making code illustrates this concept of unequal evaluations. The example below is the most basic logical decision maker, the “if/else” evaluation, and contains within it the central paradox of logic. In this evaluation, we ask the system to evaluate if a statement is true. In that case, we execute the block of code just below the if clause. If the statement evaluates false, we execute the block of code after the else keyword.
This is among the most basic of code concepts. New developers often use this idiom to create logic trees that treat if and else as equals. The developer evaluates a statement and based on its truth or falseness, takes the next step in the process. We could for example evaluate whether x in our first example equalled 4, continuing on with the script if true or generating an error if the answer is false.
But as we see in our second example, not all decisions can be made in a single evaluation. We combine two evaluations into a single clause and only if both evaluations are true can we arrive at a true statement. Critically, we arrive at a clause that treats the if and else clauses differently: the if clause treated not only as the true clause, but also as the more specific clause:
The Principles of Boolean Thinking
So what is the upshot of all this boolean determination? Does the fact that false represents a larger subset than true mean anything practical in the real world? How can we improve the way we approach projects and communication better by understanding this idea? Here are a few very important take-aways:
- While true and false represent two subsets of an entire range possibilities, if and else clauses yield only two actions with which to treat the subsets.
- Because we can evaluate a statement true only when we can specifically identify it as true, that subset of possibilities includes statements about which we know a lot.
- Because anything that does not evaluate to true is therefore false, we know relatively little about this set. We cannot assume anything about this result set, including whether the statement exists within the range at all!
That last bit is important to understand: while our Venn diagram was a closed system, most things in life exist out in the open, in the midst of a nearly-limitless set of possibilities.
This all adds up to a basic tenet: else statements are inherently weak and unreliable. Contrary to our original assumption, code does not work as effectively on both sides of the boolean divide, at all. We cannot know anything with certainty about else statements, therefore what we do with those statements must be limited and generic. The only place for an else statement to lead is either an error or else a new interrogation, altogether. But one way or another, you just can’t trust ’em.
In Agile development, we are trained to tell stories about the work we need to get done. “As a [role], I need [goal] so that [reason].” Taking that idea one step further, we can describe our desired result as a simple if/then logical tree to better understand the relative complexity of our request.
Let’s walk through a set of Story statements to see how this might work.



